This course covers the development of analysis of functions of a real variable, including rigorous proofs of results in single-variable calculus. Topics include formal treatment sequences and subsequences, series limits, pointwise and uniform continuity, sequences and series of functions, pointwise and uniform convergence, differentiation and integration of power series, the mean value theorem, Taylor expansions, the Riemann integral, and the fundamental theorem of calculus. Students gain an understanding of basic point set topology, with a focus on the theory and structure of compact and connected sets. This course involves significant analysis and construction of mathematical proofs.
Course Number
UM115
Level
University
Semester
Fall
Credit per Semester
5.00
Subject
Prerequisites
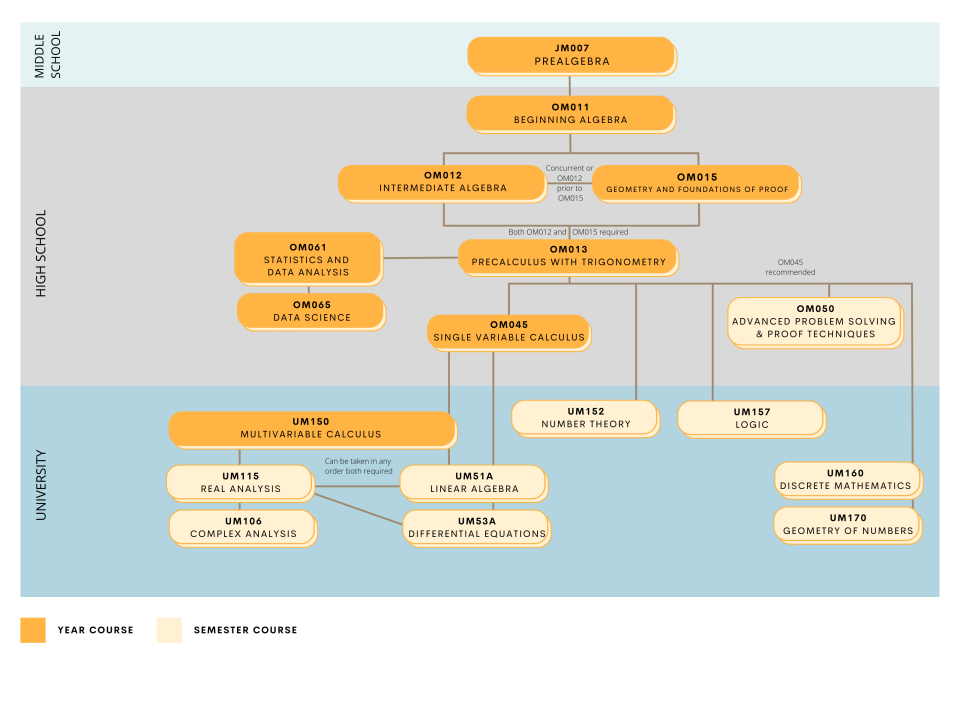
Multivariable Calculus (UM150) and Linear Algebra (UM51A), or Consent of instructor; Advanced Problem Solving & Proof Techniques (OM050) recommended
Additional Information
This course is heavily proof based.