Theory of differentiation and integration of functions of a complex variable. Topics include a formal introduction to the complex numbers and complex plane, theory of analytic functions, the Cauchy integral formula, power series and Laurent series, calculation of residues and applications, conformal mapping, and harmonic functions. Students will develop the geometric interpretation of complex functions, and use the Residue Theorem to evaluate definite integrals of real and complex functions.
Course Number
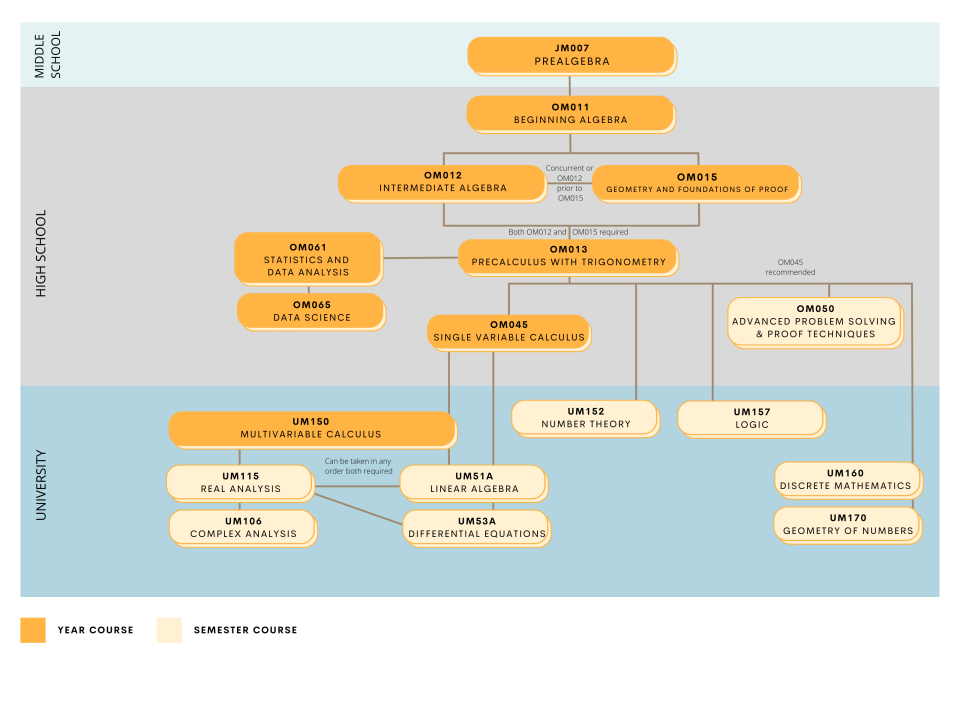
UM106
Level
University
Semester
Spring
Credit per Semester
5.00
Subject
Prerequisites
Multivariable Calculus (UM150) and Linear Algebra (UM51A), or Consent of instructor; Advanced Problem Solving & Proof Techniques (OM050) recommended