This semester-long course in theoretical mathematics develops students' facility with abstract conceptual work and prepares students for more advanced math courses relying on rigorous proofs. Students gain experience analyzing complex problem situations, formulating solutions, rigorously justifying arguments, and presenting mathematical reasoning clearly and effectively, both orally and in writing. Course topics include general guidelines for analyzing problems, proving conditional and biconditional statements, working with negations, proof by contradiction, problem-solving heuristics, understanding quantifiers, mathematical induction, the construction method, working with nested quantifiers, and special proof techniques. The course focuses on practical problem-solving and proof-construction techniques that will be invaluable in many university-level mathematics courses.
Course Number
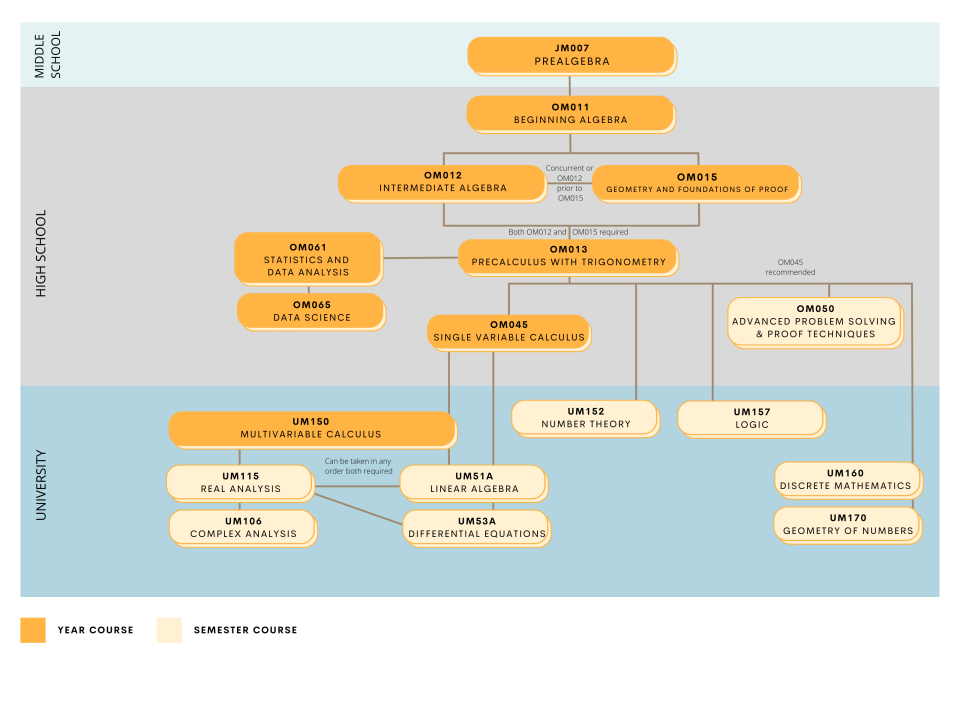
OM050
Level
High School
Semester
Fall or Spring
Credit per Semester
5.00
Subject
Prerequisites
Precalculus with Trigonometry (OM013)
Additional Information
Single Variable Calculus (OM045) or equivalent recommended